因为对一元函数来讲,可导必可微,可微必可导。但对多元函数来讲,可微是可偏导的充分不必要条件。
可温筝皇庥微是总体的、一般的、关于多的性质,可导是单一的、特殊的、关于“多”中的一的性质。一般成立,特殊必然成立;特殊成立,一般不一定成立,但特殊是一般的基础。在一元函数框架下,多即是一,那么特殊和一般在此条件下得到了统一。
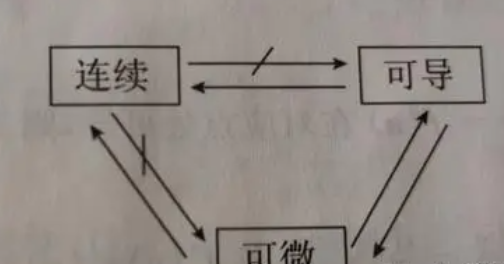
可微条件
1、必要条件
若函数在某点可微分,则函数在该点必连续;若二元函数在某点可微分,则该函数在该点对x和y的偏导数必存在。
2、充分条件
若函数对x和y的偏导数在这点的某一邻域内都存在,且均在这点连续,则该函数在这点可微。
