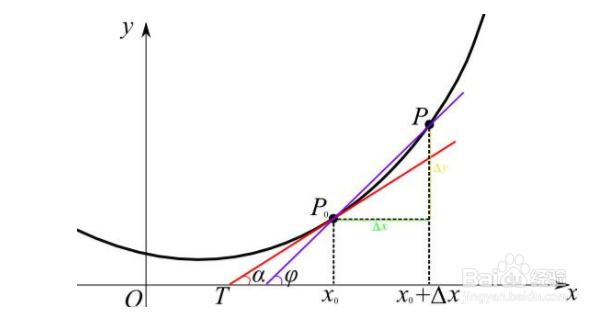
1、dy/dx是y对x的导数,dy是y的微分
y对x导数就是y的微分除以x的微分,因此导数就是微分之商,也称为微商.这两个概念是不同的。
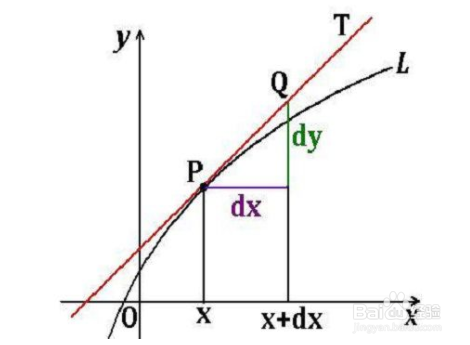
求dy就是求y的微分,如果不熟悉微分运算,可以先求dy/dx=f'(x),求完后将dx乘到右边得
dy=f'(x)dx
2、高数dy/dx
1.质点沿x轴运动速度为dx/dt=f(x),求质点的加速度a
2.dx/dy=1/y’,求二阶导数d2x/dy2
这两道题答案二阶导数为什么不是一阶导数的导数呢?
3、a=d2x/dt2=d(dx/dt)/dt
=d[f(x)]/dt
={d[f(x)]/dx}*(dx/dt)
=f'(x)*f(x)
2.
d2x/dy2=d(dx/dy)/dy
=d(1/y')/dy【这里注意y'是关于x的函数,所以先对x求导】
=[d(1/y')/dx]*(dx/dy)
={-y''/[(y')^2]}*(1/y')
=-y''/[(y')^3]
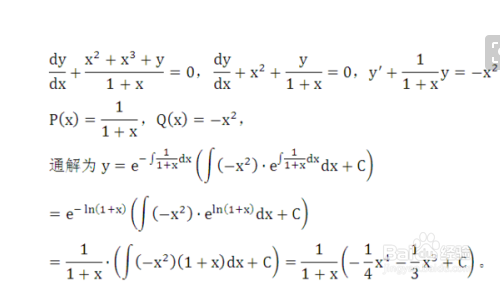
4、简单高等数学求dy/dx
x^y=y^x,y是x的函数求dy/dx答案第一步是e^(ylnx)=e^(xlny),我第一步是ylnx=xlny,后面都一样,两边对x求导,但答案为何不一样?
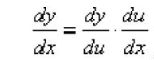
5、答案只是形式上不一样,但可以通过原来的方程x^y=y^x进行互化,所以本质上是相同的。
方程确定的隐函数的导数,结果的特点:1、一般含有因变量;2、结果形式上不唯一,也就是有多种形式的结果。

