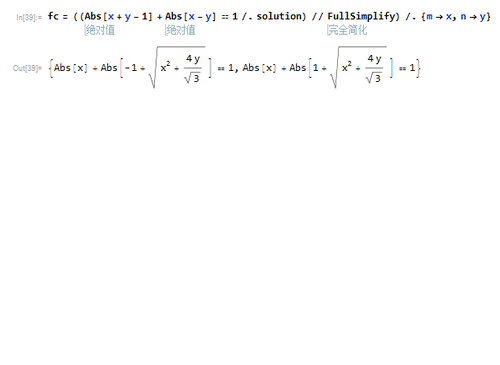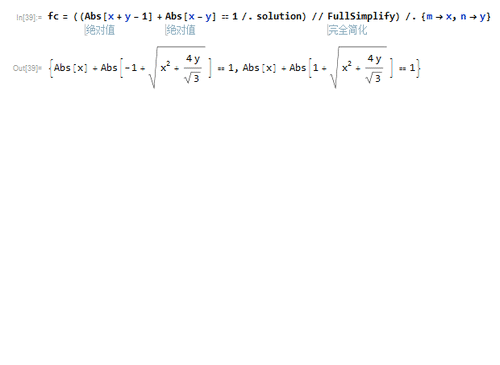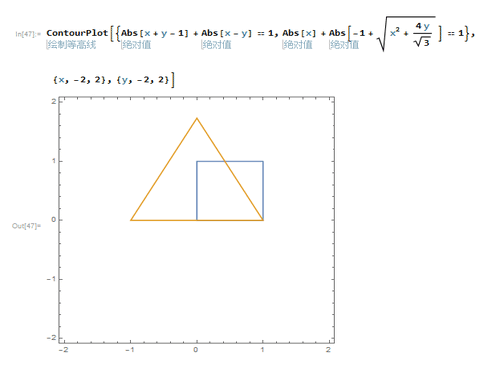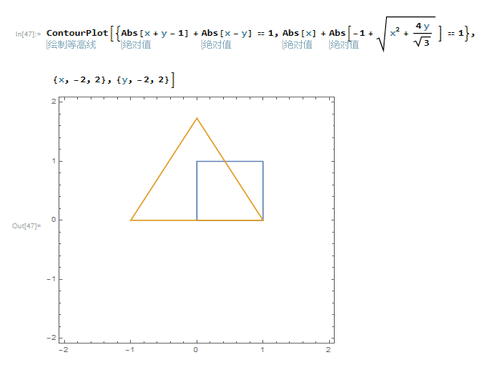1、以A(0,0)、B(0,1)、C(1,1)、D(1,0)为顶点的正方形的参数方程是:{Abs[Cos[t]] Cos[t] + Abs[Sin[t]] Sin[t] + 1, Abs[Cos[t]] Cos[t] - Abs[Sin[t]] Sin[t] + 1}/2
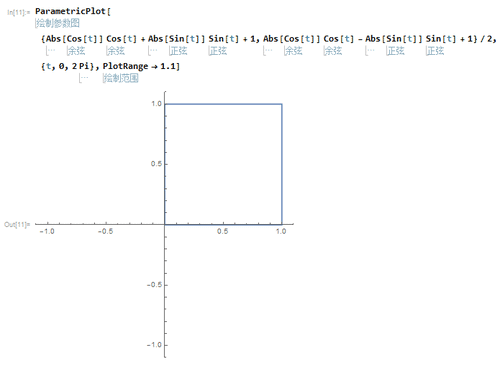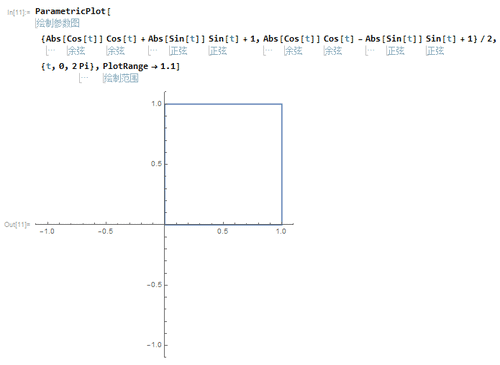
2、按照坐标变换的规则(x→x-y,y→sqrt(3)*x*y),对参数方程进行变换,就可以得到正三角形的参数方程:Abs[Sin[t]] Sin[t], Sqrt[3] Cos[t] (Abs[Cos[t]] + Cos[t])/2

3、把正方形和正三角形都画出来。
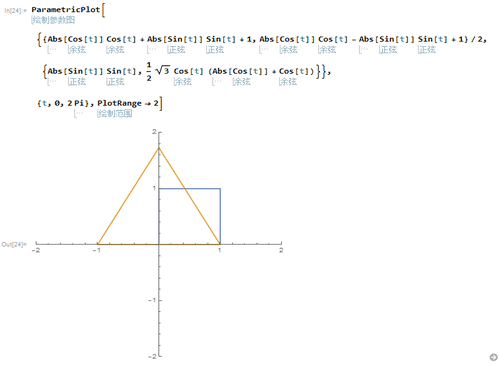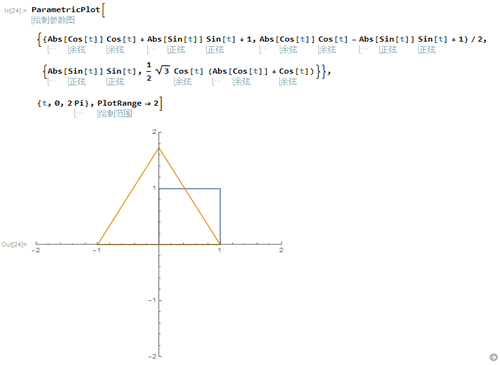
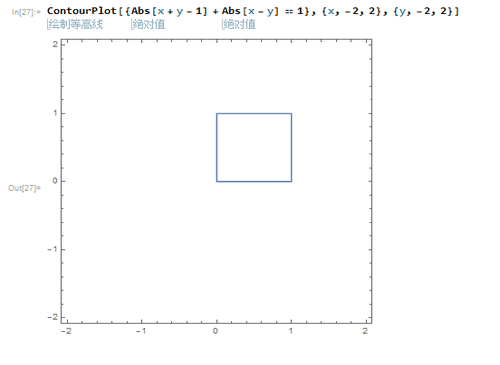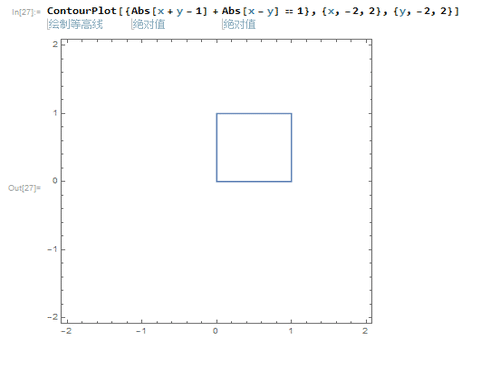
4、以A(0,0)、B(0,1)、C(1,1)、D(1,0)为顶点的正方形的隐函数方程是:Abs[x + y - 1] + Abs[x - y] == 1
5、根据(x→x-y,y→sqrt(3)*x*y)的逆变换,就可以求出正三角形的隐函数方程。先计算逆变换:solution = Solve[{m == x - y, n == Sqrt[3]*x*y}, {x, y}]

6、把逆变换带入到正方形的隐函数方程里面,就得到正三角形的项滓呶茉隐函数方程:Abs[x] + Abs[-1 敫苻匈酃+ Sqrt[x^2 + (4 y)/Sqrt[3]]] == 1或者Abs[x] + Abs[1 + Sqrt[x^2 + (4 y)/Sqrt[3]]] == 1注意第二个方程式,当x和y都是实数的时候,左边显然≥1,当且仅当x=y=0的时候,才能取等号,所以,真实代表正三角形的方程是第一个方程式。