1、三角积化和差的公式如下:

1、∫sin(ax+b)cos(ax+b)dx,a≠0,b∈R,推导步骤如下:

2、主要步骤是,先凑分:dx=(1/a)d(ax+b),随后,用到三角积化和差公式或倍角公式变形。
1、此时为a=2,b=1的情形。
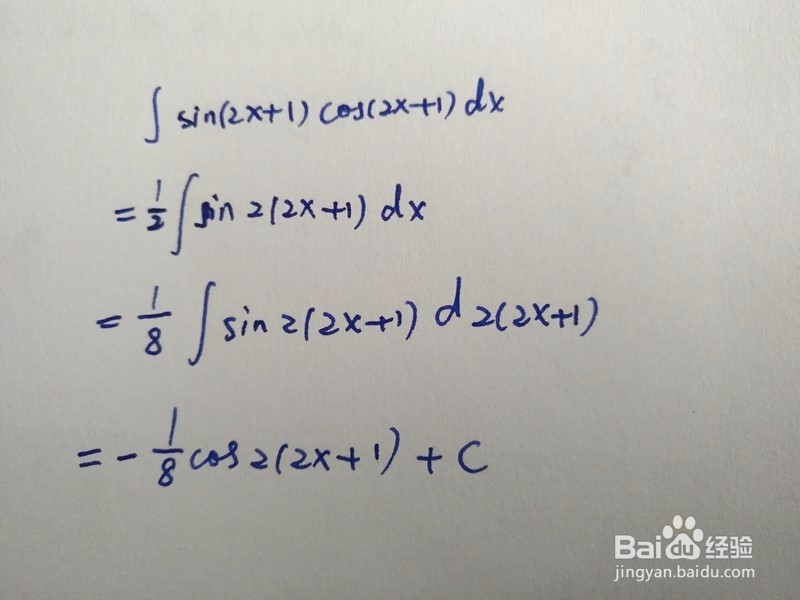
2、凑分步骤中:dx=(1/2)d(2x+1)
3、倍角公式为:
sin(2x+1)cos(2x+1)=(1/2)sin2(2x+1).
1、此时为a=-1,b=1.

2、凑分步骤中:dx=-d(-x+1)
3、sin(1-x)cos(1-x)=(1/2)sin2(1-x).
1、本例子中,a=1,b=-1。

2、凑分步骤中:dx=d(x+1)。
3、sin(x-1)cos(x-1)=(1/2)sin2(x-1).
1、本例中a=-2,b=1。

2、凑分步骤中:dx=(-1/2)d(1-2x)。
3、sin(1-2x)cos(1-2x)=(1/2)sin2(1-2x).
1、本例中a=2,b=m。

2、凑分步骤中:dx=(1/2)d(2x+m)。
3、sin(2x+m)cos(2x+m)=(1/2)sin2(2x+m).
1、本例中a=2,b=y。

2、凑分步骤中:dx=(1/2)d(2x+y)。
3、sin(2x+y)cos(2x+y)=(1/2)sin2(2x+y).
