1、Max Z=6*x1-2*x2+3*x3s.t.[2*x1-x2+2*x3<=2; x1+4*x3<=4; x1,x2,x3>=0;]题目如上述所示。
2、将题目所给出的约数方程,化为标准型方程(将<=引入约数方程变成=),构造等式。

3、将标准型化成单纯形表,取人大于零且最大的进行出基变量,在根据最后一列比值,选出出基变量,在本题中出基变量为2.
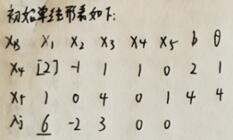
4、然后先把1/2所在行进行整理,将1/2变成1,然后对1/2所在列进行整理都化成0。得出如下图所示情形。

5、根据上图在选出进基变量和出基变量,在上式中出基变量为1/2.
6、根据第五部整理后如下图所示,此时发现人没有大于0的正值,所以没有办法进基,这时可以看出x1=4,x2=6.

7、所以最后的最终解如下;

