1、模块一:
1.计算机中的浮点数一般都是用二进制表示的。如果在不同的计算机中,浮点数采用不同的基数、尾数和阶码的长度,则浮点数表示有较大的差别,这样不利于软件在不同的机器之间的移植。从20世纪70年代末开始,IEEE就成立了一个专门的委员会负责对浮点数进行标准化。IEEE754标准是1985年由IEEE提出的一个从系统结构角度支持浮点数表示的标准,当今流行的计算机几乎都采用这一标准。
在目前常用的80X86系列微机中,通常设有支持浮点运算的部件。在这些机器中的浮点数采用IEEE754标准,按IEEE754标准,常用的浮点数的格式如图所示。


2、2.短浮点数又称为单精度浮点数,长浮点数又称为双精度浮点数,它们都采用隐含尾数最高数位的方法,这样,无形中又增加了一位尾数。临时浮点数又称为扩展精度浮点数,它没有隐含位。
在IEEE754标准中阶码用移码表示,尾数用原码表示,隐含的基数为2。下表总结了短浮点数(32位)和长浮点数(64位)格式的有关参数。

3、3.以短浮点数为例,阶码最大值为127,最小值为-126,则阶码移码的表示范围为1~254。这是因为阶码为全0和全1这两种极端阶码值用于定义特殊数值:机器零和无穷大。
非0规格化数的尾数的最高有效位一定为1。IEEE754标准规定规格化浮点数在小数点的左边有一隐含位(作为二进制整数的个位数)。由于该位为1,不需要存储,在运算时,自动加上该位参加运算,因此尾数实际上是24位。此时规格化浮点数的尾数为1.f(f为尾数,1为隐含位),所表示的规格化浮点数为
士(1.f)×2^(E-127)。
4、4.下面以32位的短浮点数为例,讨论浮点代码与其真值之间的关系。最高位为数符位;其后是8位阶码,以2为底,用移码表示,阶码的偏置值为127;其余23位是尾数数值位。对于规格化的二进制浮点数,数值的最高位总是“1”,为了能使尾数多表示一位有效值,可将这个“1”隐含,因此尾数数值实际上是24位(1位隐含位+23位小数位)。应注意的是,隐含的1是一位整数(即位权为20)。在浮点格式中表示出来的23位尾数是纯小数,用原码表示。例如,(12)10=(1100)2,将它规格化后结果为1.1×2^3,其中整数部分的“1”将不存储在23位尾数内。
阶码是以移码形式存储的。对于短浮点数,偏置值为127(3FH);对于长浮点数,偏移量为1023(3FFH)。存储浮点数阶码部分之前,偏置值要先加到阶码真值上。上述例子中,阶码真值为3,故在短浮点数中,移码表示的阶码为127+3=130(82H);长浮点数中,为1023+3=1026(402H)。
5、5.例1:将(100.25)10转换成短浮点(单精度)数格式。
(1)把十进制数转换成为二进制数
(100.25)10=(1100100.01)2
(2)规格化二进制数
1100100.01=1.10010001×2^6
(3)计算出阶码的移码(公式:[X]移码=偏置值+X(真值),X(真值)=[X]移码-偏置值)
1111111+110=10000101
(4)以短浮点数格式存储该数
因为,符号位=0阶码=10000101尾数=10010001000000000000000所以,短浮点数代码为
0;10000101;10010001000000000000000表示为十六进制的代码:42C88000H。
例2:把短浮点数C1C90000H转换成为十进制数。
(1)将十六进制代码写成二进制形式,并分离出符号位、阶码和尾数。
因为,C1C90000H=11000001110010010000000000000000所以,符号位=1阶码=10000011尾数=10010010000000000000000
(2)计算出阶码真值(阶码真值+偏置值=移码 阶码真值=移码-偏置值)
10000011-1111111=100
(3)以规格化二进制数形式写出此数:1.1001001×2^4
(4)写成非规格化二进制数形式:11001.001
(5)转换成十进制数,并加上符号位
(11001.001)2=(25.125)10所以,该浮点数=-25.125
通常,将IEEE754短浮点数规格化的数值v表示为:
v=(-1)^Sx(1.f)×2^(E-127)
其中,S代表符号位,来自符号的英语单词Sign,其中S=0表示正数,S=1表示负数;E为用移码表示的阶码;f是尾数的小数部分。
为了表示∞和一些特殊的数值,E的最小值0和最大值255将留作它用。因此,最小正常的E=1,最大正常的E=254,所以短浮点数的阶码真值的取值范围为-126~127。当E和m均为全0时,表示机器零;当E为全1,m为全0时,表示士∞。
1、模块二:短浮点数(单精度)实验证明
1.在VC++6.0加以验证单精度浮点数存储形式
#include "stdio.h"
void main()
{
float a[]={100.25};
float b[]={-25.125};
return;
}
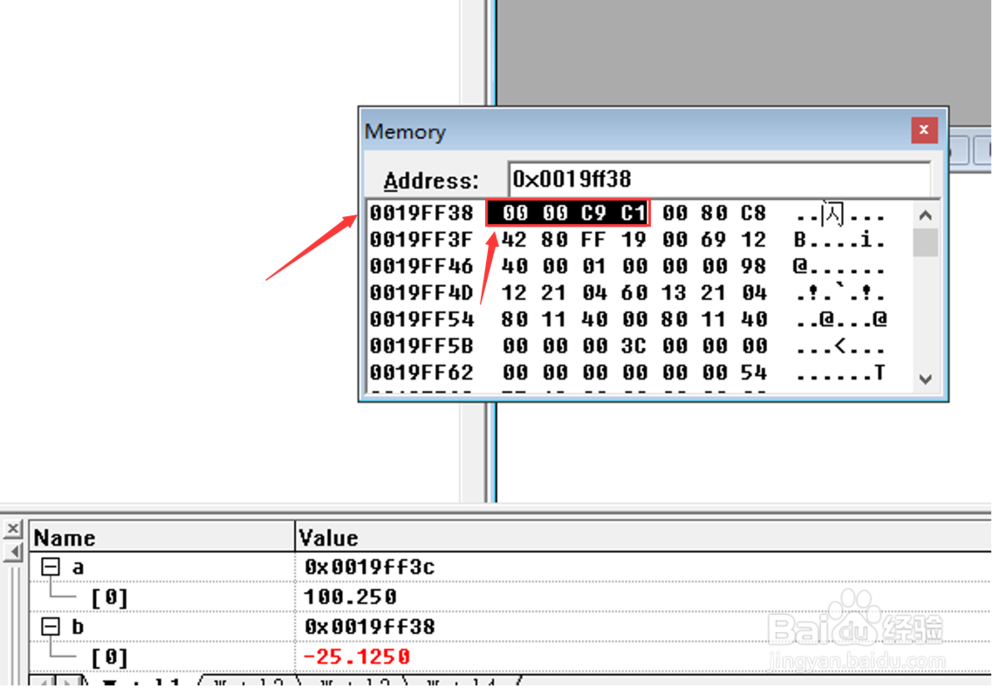
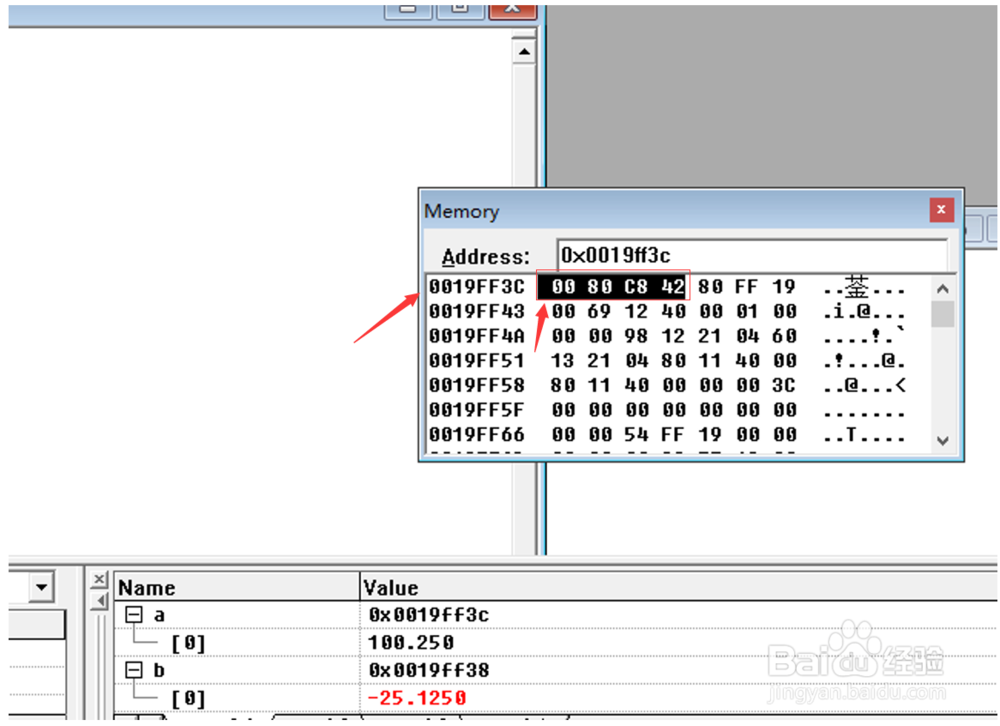
输入如图代码,然后按下(CTRL+F7)编译代码, 然后按下F9键,每条语句前插入断点(INSERT BREAK POINT),然后按下F11键,逐条运行(STEP INTO),如图所示:在代码编辑窗口中,将两个变量的名称a,b用鼠标别拖拽到Watch1窗口中,然后在菜单栏空白处,单击鼠标右键,选中DEBUG(调试窗口)及MEMORY(内存窗口)及WATCH(查看窗口)选项,然后在MEMORYP窗口地址栏中输入变量a和b的地址,然后就可以看到变量a,b的以十六进制形式存储单精度浮点数的值,按下shift+F5(stop debugging),调试完毕,,如图所示:
2、2.
双精度(长浮点数)的验证过程:
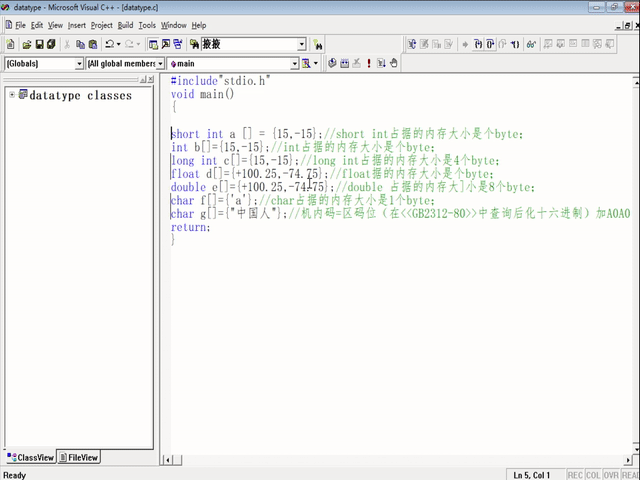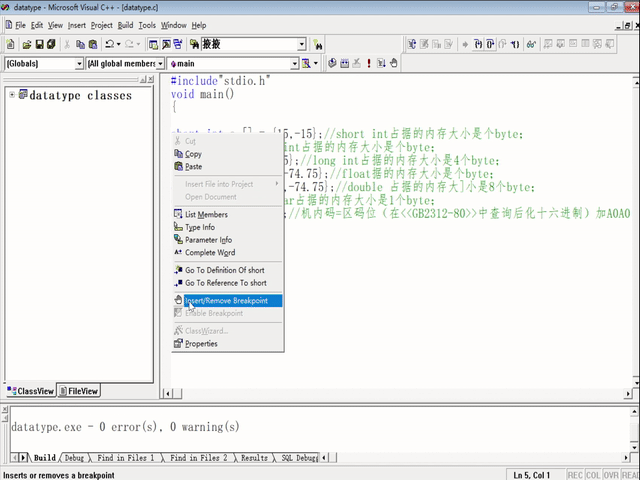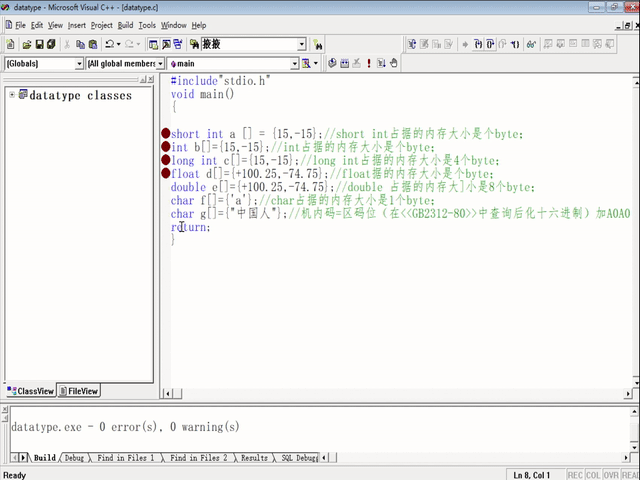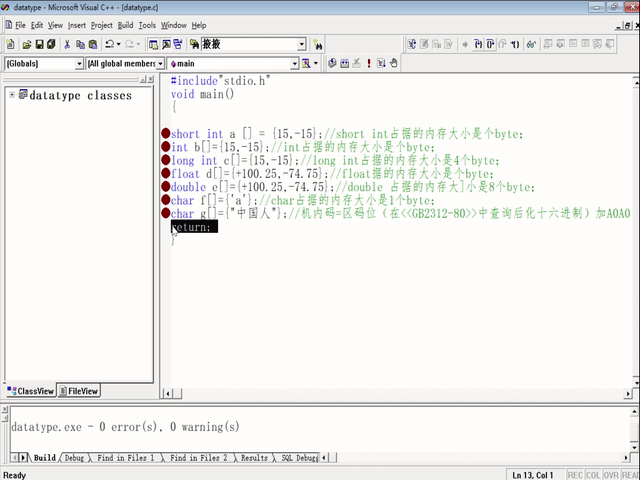
在VC++6.0中输入Data type .c的内容如下:
#include"stdio.h"
void main()
{
short int a[]={15,-15};//short 占据的内存大小是2 个byte;
int b[]={15,-15};//int占据的内存大小是4 个byte;
long int c[2]={15,-15};//long占据的内存大小是4 个byte;
float d[]={ +100.25,-74.75};//float占据的内存大小是4 个byte;
double e[]={+100.25,-74.75};//double 占据的内存大小是8个byte;
char f[]={'a'};//char占据的内存大小是1 个byte;
char g[]={"中国人"};//机内码=区码位(在GB2312-80中查询以后转换为十六进制)加A0A0(十六进制)
return;
}
输入如图代码,然后按下(CTRL+F7)编译代码, 然后每条语句前插入断点(INSERT BREAK POINT),按下F9键,然后按下F11键,以保证逐条语句运行(STEP
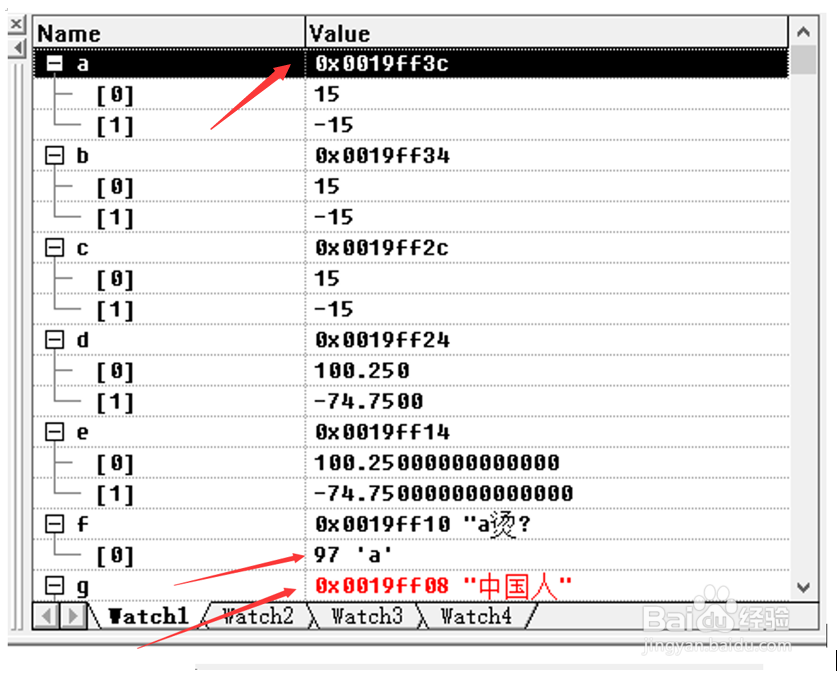
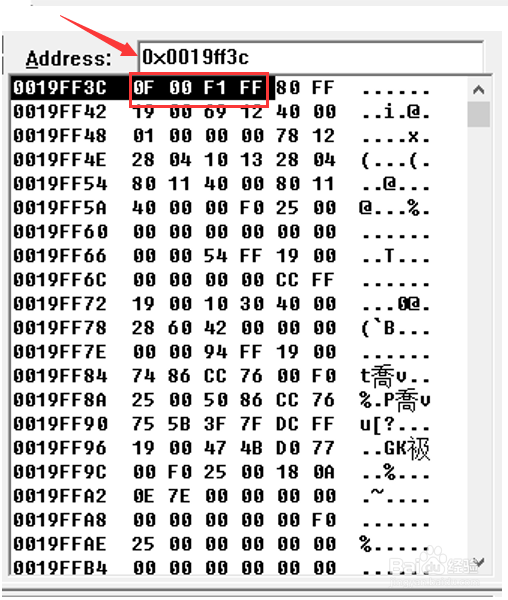
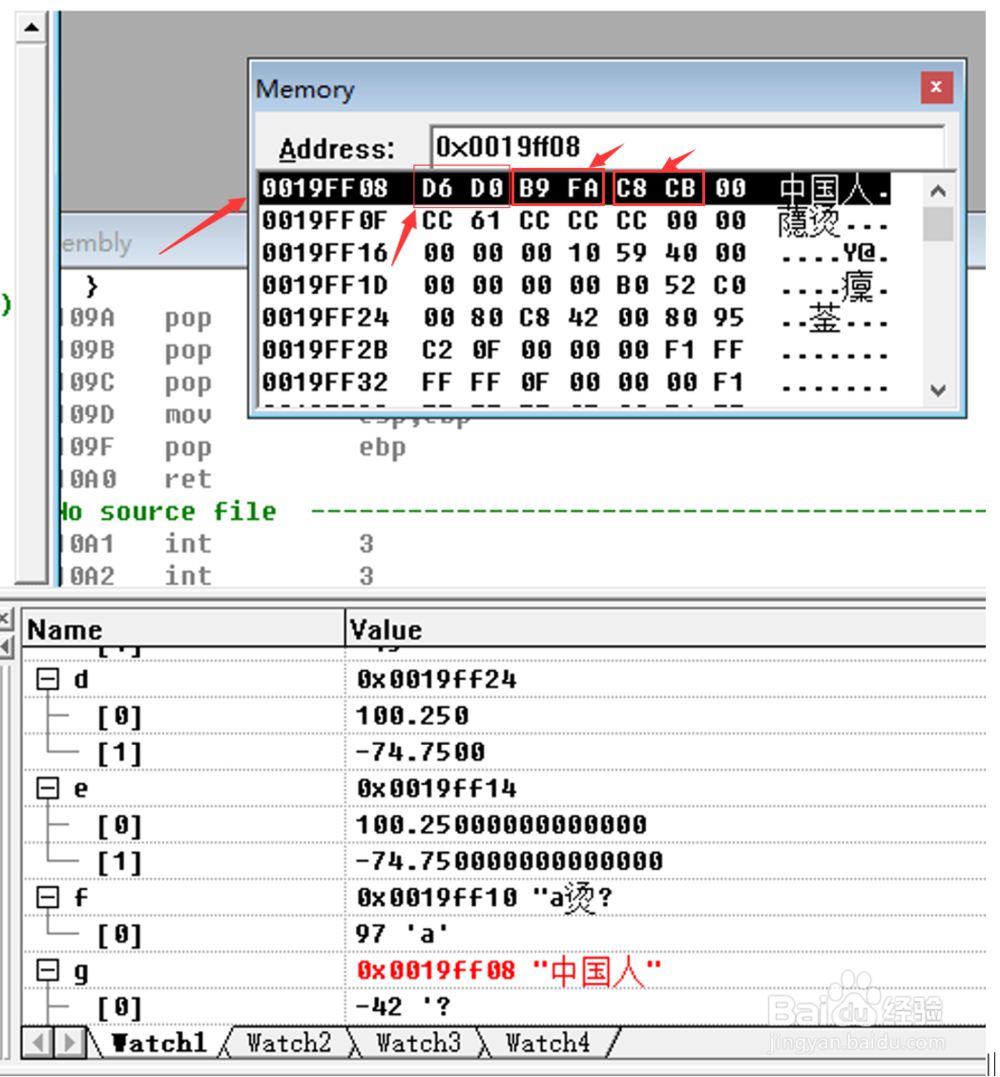
INTO), 在代码编辑窗口中,将两个变量的名称a,b,c,d,e,f,g用鼠标别拖拽到Watch1窗口中,然后在菜单栏空白处,单击鼠标右键,选中DEBUG(调试窗口)及MEMORY(内存窗口)及WATCH(查看窗口)选项,每次运行一条语句,就在MEMORY窗口地址栏中分别输入当前变量的地址,然后就可以看到变量a,b ,c,d,e,f,g的以十六进制形式存储单,双精度浮点数的值,在MEMOEY(内存)窗口输入每个数组的存储十六进制地址,比如变量”a”数组的存储地址为0x0019ff3c,存储形式为0F00H,(注意存储方式为大端存储(big endian),左边为高位字节,实际为000FH,因为第8位的符号位为0(代表是正数)所以要扩展成16位(2字节)时,需将最高位的符号位作填充,所以另一个字节,就变成了00H了, 注意变量是整数时,整数的存储形式是一位符号位的补码形式,特别注意补码时符号位“0”(正数),或“1”(负数)向左边高位扩充作为全部符号位的规律,变量”f”为1个字节的字符型,它在内存中的地址是0x19ff10,存储的内容为十六进制数61H,通过查询ASCII表, 知道就是相当于字符’a’的ascii码的十进制数97,按下shift+F5(stop debugging),调试完毕,如图所示:
3、3.在工具栏中找到WATCH及MEMORY窗口,变量:a","b","c","d","e","f","g"的内存地址以及相应项所保存的值,如图所示:
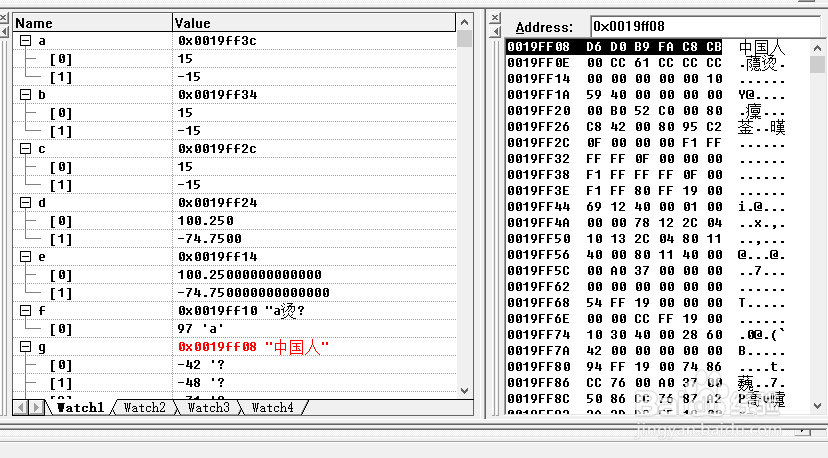
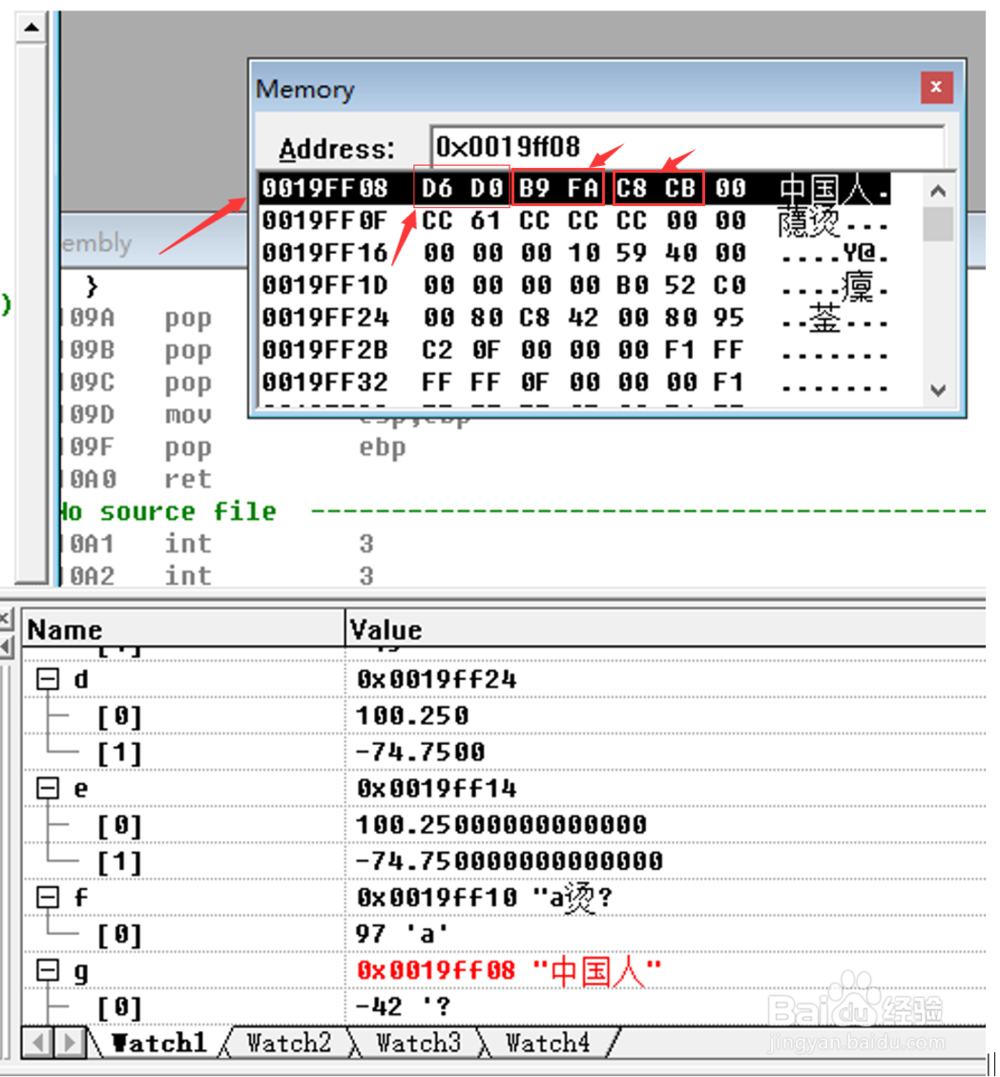
4、4.下面讲解自变量”g”的内容:我们可以通过查询<<GB2312-80>>编码表以后,计算出”中国人”字符的值,过程如下:
在GB2312-80国家标准文档中查找汉字的区位号,以“中”字为例。
查询GB2312-80编码表。得到“中”字位于第54区,第48位(位号为左边的行号为”4”加上上面的列号为”8”,组合成48)。
5、5.将“中”字的区号和位号分别转换为十六进制,得到它的区位码,十进制化十六进制,可以用windows系统自带的计算器,选择程序模式。
区号:54=36H 位号:48=30H
则“中”字的区位码为:3630H。
(3)将区位码加上2020H 即得到它的国标码。
则“中”字的国标码为:5650H。
如下图所示:

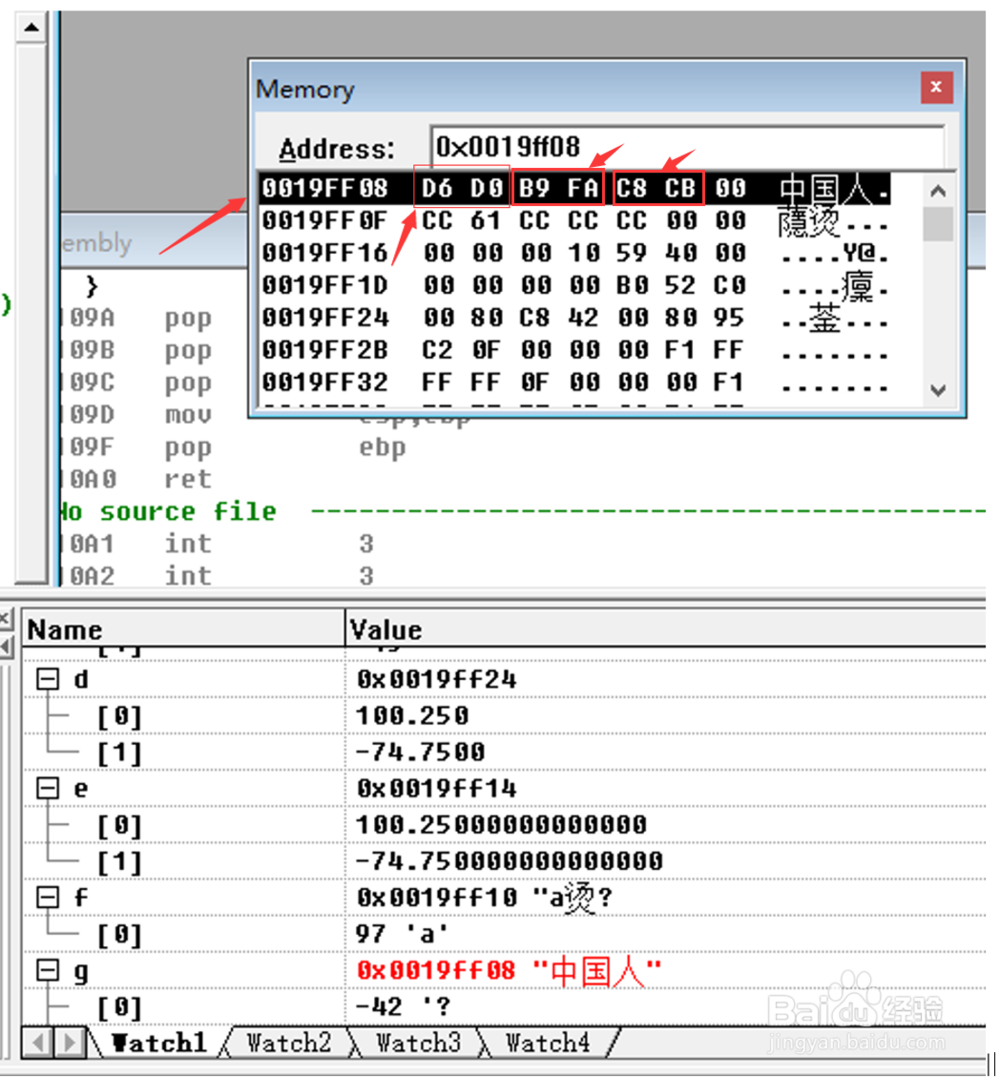
6、6.将国标码加上8080H 即得到它的机内码(在计算机中的存储形式)。
则“中”字的内码为:D6D0H。
另一种方法: 机内码=区位码+2020H+8080H=区位码+A0A0H=3630H++A0A0H=D6D0H
7、7.将“国”字的区号和位号分别转换为十六进制,得到它的区位码。
区号:25=19H 位号:90=5AH
另一种方法: 机内码= 195A H+A0A0H=B9FAH
则“国”字的区位码为: B9FAH。

8、8.将“人”字的区号和位号分别转换为十六进制,得到它的区位码。
区号:40=28H 位号:43=2BH
另一种方法: 机内码= 282B H+A0A0H=C8CBH
则“人”字的区位码为: C8CBH。

9、9.最后,我们以视频操作的方式来总结本教程中最难掌握的Debug调试过程,请特别注意操作过程中,十六进制内存地址及其相应地址以大端秩序存储的十六进制数据内容。如下二图所示:
10、9.本教程深入讲解了计算机内部的单,双精度的浮点数以IEEE754格式存储形式的原理,以及<<GB2312-80>>国标编码、内码、区位码,机内码(中文字符在计算机中的存储形式)ASCII码字符存储原理. 师者,所以传道受业解惑也。人非生而知之者,孰能无惑?惑而不从师,其为惑也,终不解矣。如对您有帮助,请不吝点击投票转发,如您有任何疑问或建议,请留言评论。
