1、判断函数的性质 下面我们就以带绝对值的正选函数f(x)=sin|x|为例来求导。先来判断一下一下该函数的性质。我们先用matlab画一下该函数的图形,具体代码如下:%画出f(x像粜杵泳)=sin|x|图形clearx=-2*pi:pi/20:2*pi;y=sin(abs(x));plot(x,y,'r','LineWidth',1.5)title('函数f(x)=sin|x|图形'),xlabel('x'),ylabel('y') 函数图形为:

2、x≥0,有导数的定义求右导数 当x≥0时,我们可以去掉函数中的绝对值,这时候函数f就变为:f(x)=sinx,这时候求右导数就简单多了,不过还是得用定义发求右导数。具体代码以及计算结果请看下图:

3、x≤0,由导数的定义求左导数 同理,当x≤0时,去掉函数中的绝对值,f就变为:f(x)=sin(-x).。用定义发求左导数。具体代码以及计算结果请看下图,有图上的结果再结合上一部结论可以得出,f(x)在x=0点的导数不存在,而且在小于0的区间和大于0的区间导数不一致。

4、直接利用diff求导matlab提供了一个直接求函数导数的指令diff,然而当函数含有绝对值时候是否还有效呢?我们来探索一下。有下图中可以看出,当x=0时,函数的导数出现了错误的结果。

5、画出图形代码 下面我们画出函数f(x)、两个区间分别的导数图形。具体代码如下图所示:
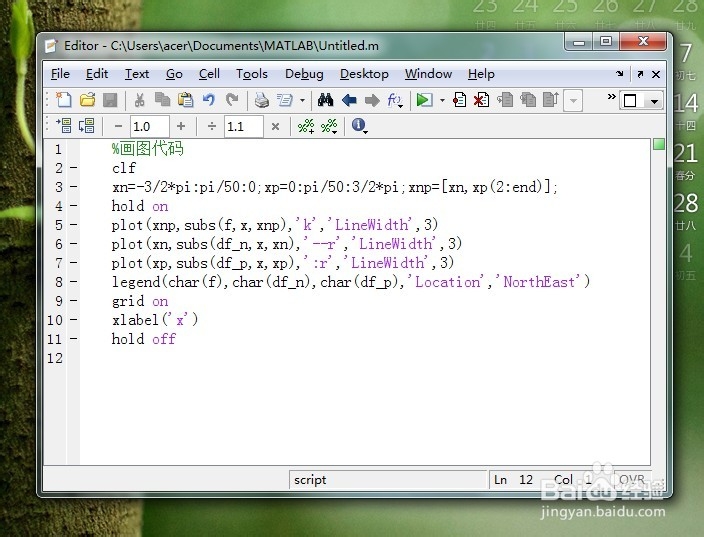
6、画出的图形如下图所示:

